MILR: Improving Multimodal Image Generation via Test-Time Latent Reasoning

Yapeng Mi^1,4, Hengli Li^2,4, Yanpeng Zhao⁴^✉, Chenxi Li^3,4, Huimin Wu⁴, Xiaojian Ma⁴, Song-Chun Zhu^2,4, Ying Nian Wu⁵, Qing Li⁴^✉

¹University of Science and Technology of China, ²Peking University, ³Tsinghua University, ⁴BIGAI, ⁵University of California, Los Angeles

arXiv Code

Figure 1. Latent reasoning of MILR. The black solid line denotes extracting the output vector representations $z^{k}$ of the text tokens $z^{(t)}$ and image tokens $z^{(v)}$ to be optimized, and the black dashed line denotes decoding from the optimized latent vectors $z^{k+1}$, where $z=[z^{(t)},z^{(v)}]$.

Introduction

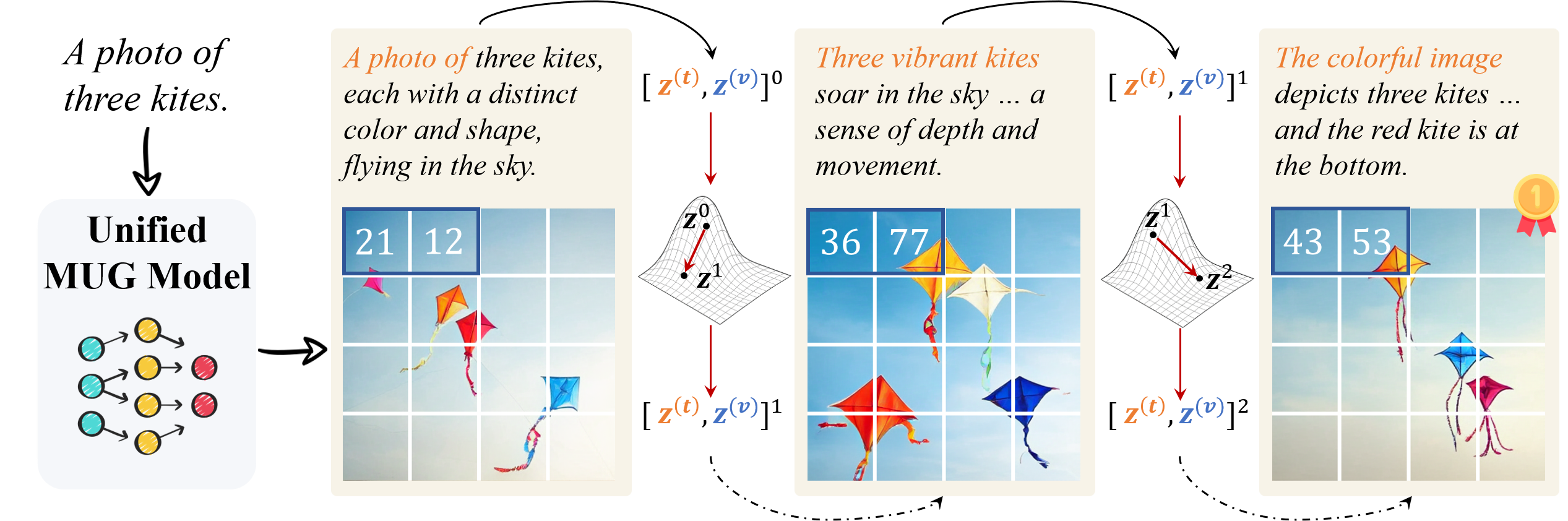
Reasoning-augmented machine learning systems have shown improved performance in various domains, including image generation. However, existing reasoning-based methods for image generation either restrict reasoning to a single modality (image or text) or rely on high-quality reasoning data for fine-tuning. To tackle these limitations, we propose MILR, a test-time method that jointly reasons over image and text in a unified latent vector space. Reasoning in MILR is performed by searching through vector representations of discrete image and text tokens. Practically, this is implemented via the policy gradient method, guided by an image quality critic. We instantiate MILR within the unified multimodal understanding and generation framework that natively supports language reasoning before image synthesis and thus facilitates cross-modal reasoning. The intermediate model outputs, which are to be optimized, serve as the unified latent space, enabling MILR to operate entirely at test time. We evaluate MILR on GenEval, T2I-CompBench, and WISE, achieving state-of-the-art results on all benchmarks. Notably, on knowledge-intensive WISE, MILR attains an overall score of 0.63, improving over the baseline by 80%. Our further analysis indicates that joint reasoning in the unified latent space is the key to its strong performance. Moreover, our qualitative studies reveal MILR's non-trivial ability in temporal and cultural reasoning, highlighting the efficacy of our reasoning method.

Image Generation via Test-time Latent Reasoning (MILR)

Figure 2. Overview of MILR. MILR performs test-time latent reasoning in a unified latent space; it uses policy gradients to iteratively refine text & image latents $z^{(t)}$, $z^{(v)}$, guided by a reward model.

Multi-Modal Latent Reasoning

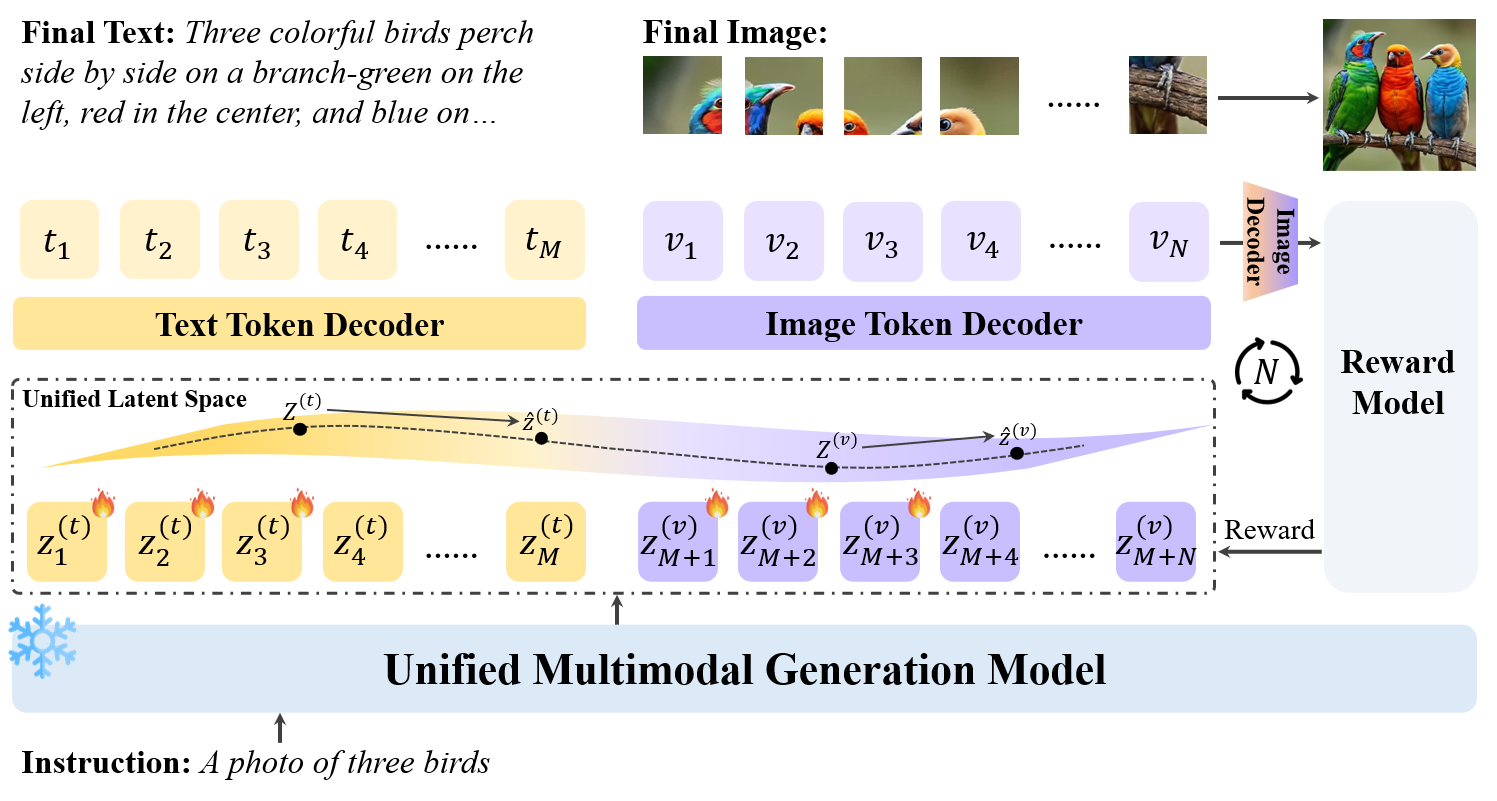
Formally, denoting the latent representations of image and text tokens by $ \mathbf{z}^{(v)} = z^{(v)}_{1:N} $ and $ \mathbf{z}^{(t)} = z^{(t)}_{1:M} $, respectively, where $ z^{(v)}, z^{(t)} \in \mathbb{R}^{d} $ are the outputs from the same Transformer layer and thus lie in a shared $ d $-dimensional vector space. The goal of latent reasoning is to find an optimal latent representation that maximizes the expected reward under $ p(\cdot \mid \mathbf{z}, c) $ without modifying any model parameters; we can therefore write the reasoning target as:

$$ \mathbf{z}^{*} = \arg\max_{\mathbf{z}} \mathbb{E}_{V_f \sim p(\cdot \mid \mathbf{z},\, c)} \big[ R(V_f, c) \big] $$

where $ \mathbf{z} = [\mathbf{z}^{(t)};\mathbf{z}^{(v)}] $ indicates the multimodal latent representation of the token sequence $ [\mathbf{t}, \mathbf{v}] $. We refer to this optimization problem as multimodal latent reasoning. Given the optimal $ \mathbf{z}^{\star} $ from a specific model layer, to produce the final $ V_f $, we continue the forward pass until it is decoded into discrete tokens $ [\mathbf{t}, \mathbf{v}] $. Thus, the pixel image generation becomes:

$$ p(V_f \mid \mathbf{z}^*, c) \;=\; p\!\left(V_f \mid \mathbf{t}, \mathbf{v}, c\right)\; p\!\left(\mathbf{t}, \mathbf{v} \mid \mathbf{z}^*\right) $$

where $ p(\mathbf{t}, \mathbf{v} \mid \mathbf{z}^*) $ represents the remaining forward pass of MUG starting with $ \mathbf{z}^* $.

Gradient-based Optimization for Latent Reasoning

In general, the objective above has no closed-form solution, so we use REINFORCE, a policy-gradient method. Prior work applies it to fully textual reasoning; here we extend it to unified multimodal latent reasoning for image generation. With REINFORCE, the cross-modal update is:

$$ \mathbf{z}^{k+1} \leftarrow \mathbf{z}^{k} + \eta \cdot \mathcal{J}(\mathbf{z}^{k}), $$

$$ \mathcal{J}(\mathbf{z}^{k}) = \mathbb{E}_{V_f \sim p(\cdot \mid \mathbf{z}^{k},\, c)} \Big[ R(V_f, c)\, \nabla_{\mathbf{z}} \log p(\mathbf{t}, \mathbf{v} \mid \mathbf{z}^{k}) \Big]. $$

Here, $ \eta $ is the learning rate. For efficiency, we take $ \mathbf{z} $ from the last Transformer layer (inputs to the modality-specific decoding heads). We approximate $ \mathcal{J}(\mathbf{z}) $ with a single sampled pair $ (\mathbf{t}, \mathbf{v}) $. Gradients back-propagate only to the outputs $ \mathbf{z} $, leaving model parameters unchanged, making MILR a test-time reasoning method.

Naively, we would optimize all $ M+N $ latents in $ \mathbf{z}_{1:M+N} $, but searching using only the guidance of a reward model is potentially biased and does not leverage MUG’s generative capacity for exploration. Instead, we optimize only the first $ \lambda_{t} M $ latents for text with $ \lambda_{t}\in(0,1] $); after decoding them into discrete tokens, we complete textual reasoning via standard autoregressive generation conditioned on them. For visual reasoning, we adopt a similar strategy and optimize the first $ \lambda_{v} N $ latents with $ \lambda_{v}\in(0,1] $), consistent with observations that the first few tokens govern global image structure while the remaining tokens primarily influence high-frequency details. The full algorithm is shown below.

Experiments

Main Results

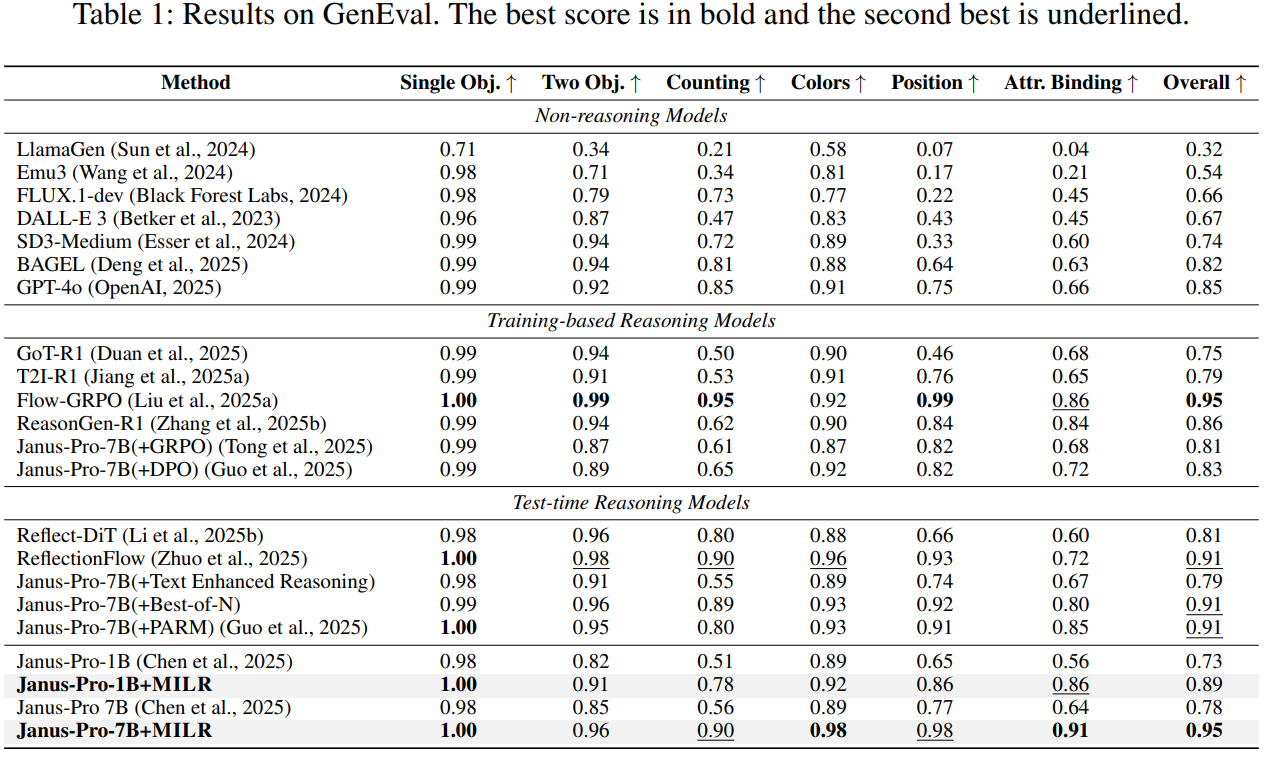
MILR achieves state-of-the-art results on GenEval, one of the most widely-used benchmarks for image generation (see Table 1). It improves over the base Janus-Pro-7B by 0.17, with the largest increases obtained from Counting (+0.34), Position (+0.21), and Attribute Binding (+0.27). Notably, MILR surpasses frontier non-reasoning models such as SD3-Medium, BAGEL, and GPT-4o (+12%). Compared with training-based reasoning models (e.g., GoT-R1 and T2I-R1), MILR performs better and requires no parameter tuning. For fairness, we also compare MILR with test-time reasoning models. Surprisingly, it outperforms ReflectionFlow and PARM (+4.5%) that rely on scaling up test-time computation, demonstrating the superiority of our test-time optimization method.

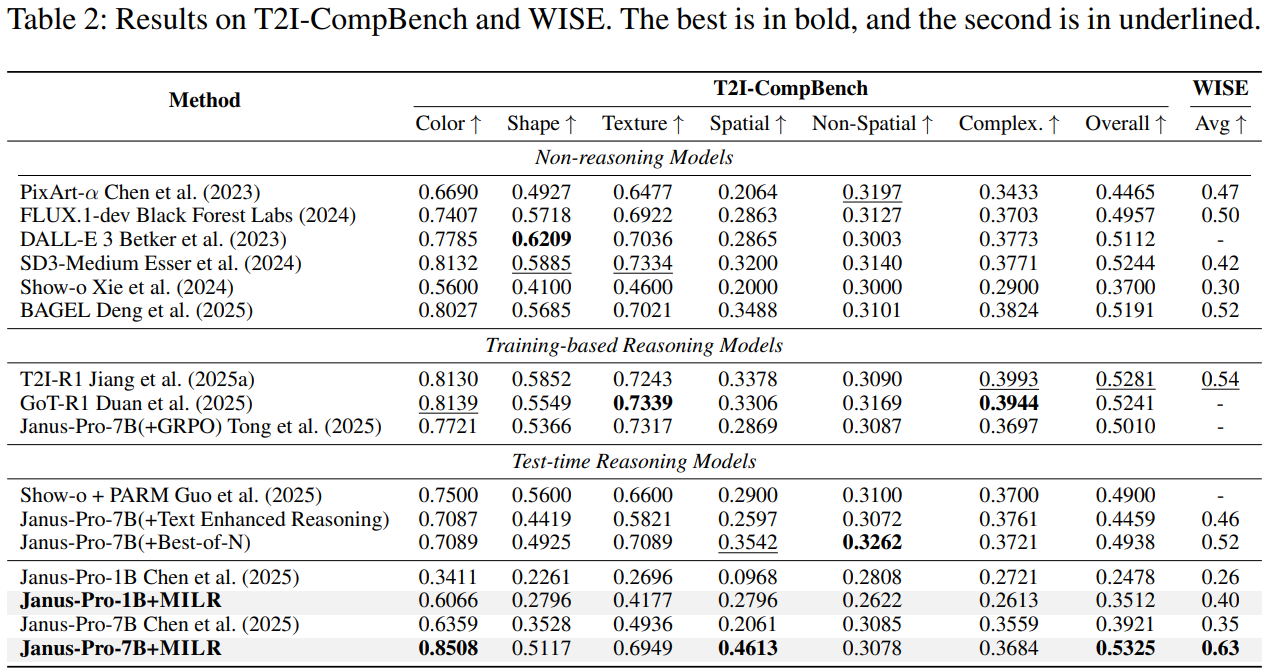
We further evaluate MILR on two additional benchmarks: T2I-CompBench and WISE (see Table 2). Again, it achieves the best performance on both, highlighting the robustness of our model. Specifically, on T2I-CompBench, MILR improves over the base Janus-Pro-7B by a large margin (+0.14) and slightly outperforms T2I-R1, a strong training-based reasoning model. On WISE, which emphasizes world knowledge understanding, MILR outperforms the base Janus-Pro-7B (+80%) and the second-best model T2I-R1 (+16.7%), implying the importance of reasoning in comprehending knowledge-intensive instructions. The case comparation is shown in Figure 3.

Figure 3. Qualitative studies on WISE. Reasoning cues are highlighted in red.

Hyperparameters Analysis

Figure 4. Performance across three benchmarks for varying optimization steps.

Figure 5. GenEval scores with varying optimization ratios of text and image tokens.

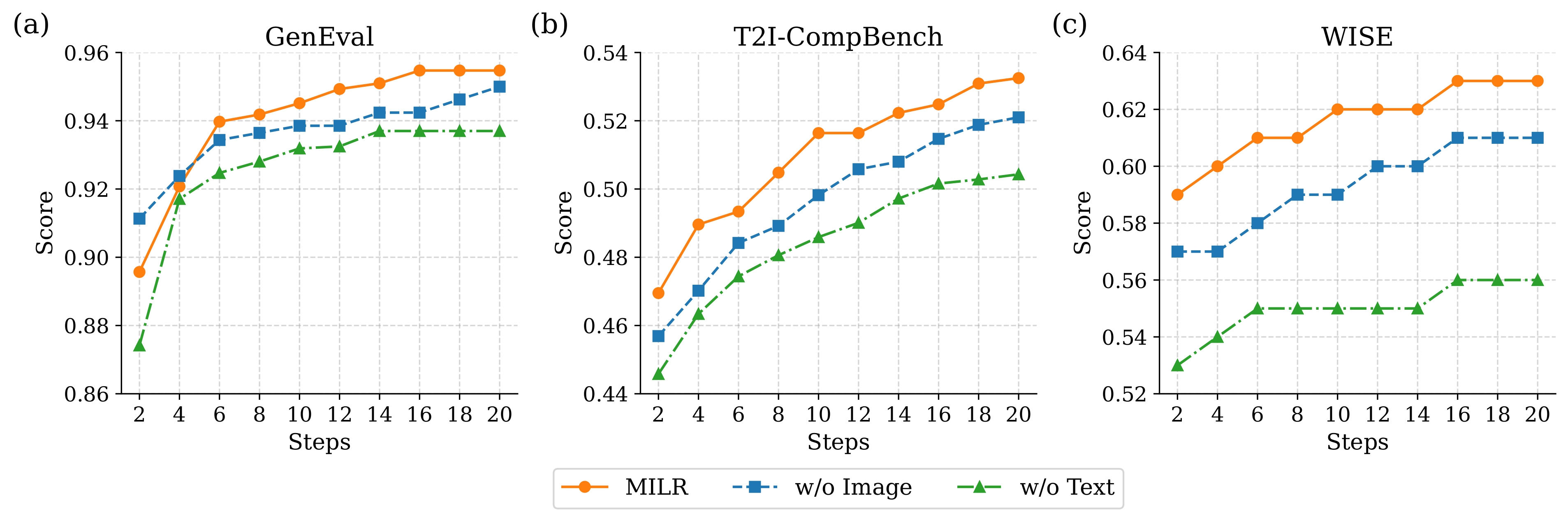
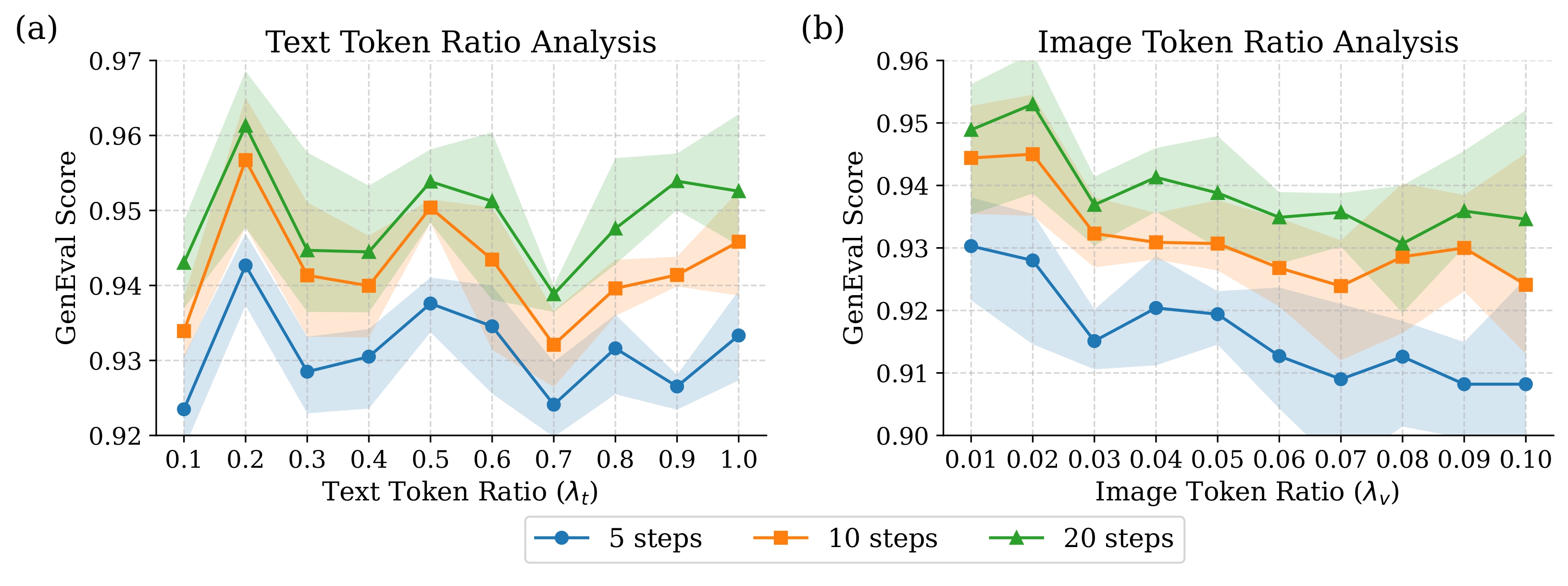
We analyze three important hyperparameters of MILR: (1) the maximum optimization step T (shown in Figure 4), (2) the portion of text tokens to be optimized λt in text-only optimization(shown in Figure 5), and (3) the proportion of image tokens to be optimized λv in image-only optimization(shown in Figure 5). And we have the following findings:

Scaling up the number of optimization steps improves performance on all benchmarks.
Optimizing a moderate amount (e.g., 20%) of text tokens leads to the best performance.
Optimizing a tiny amount (e.g., 2%) of image tokens gives rise to the best result.

Reward Models

Figure 6. Performance with different reward models on GenEval.

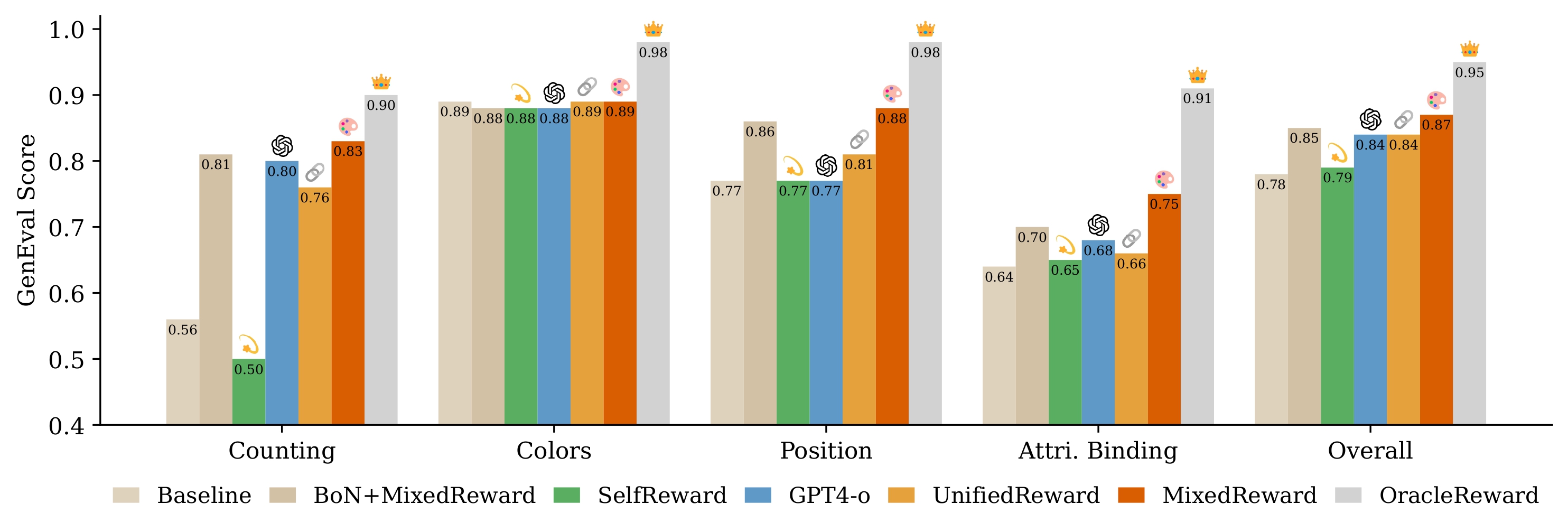
To show that MILR is effective without the reliance on OracleReward, we test it with a set of off-the-shelf reward models on GenEval:

SelfReward uses MUG itself (e.g., Janus-Pro in this work) to evaluate images.
GPT-4o represents a frontier critic for assessing image quality.
UnifiedReward is specifically tuned for a unified evaluation of MUG.
MixedReward is a composite critic for more comprehensive evaluation. It aggregates rewards from specialized models, including GroundingDINO(evaluating object detection), GIT(judging colors), and an aesthetics scorer(assessing aesthetics).

Unsurprisingly, gives rise to the best performance across all dimensions (see Figure 6). For nonoracle critics, all variants surpass the baseline in terms of the overall score. Notably, MILR remains relatively robust to different reward models, except for , which performs poorly on Counting (around 0.5). Among non-oracle critics, performs the best, suggesting that, in the absence of oracle rewards, we can derive a strong universal reward model by combining specialized critic models. Moreover, MILR+ slightly outperforms the strong Best-of-N+ baseline (+2.4%) under comparable computation (i.e., N = T = 20), once again demonstrating the superiority of our method.

BibTeX

@article{mi2025milr,
  title={MILR: Improving Multimodal Image Generation via Test-Time Latent Reasoning},
  author={Mi, Yapeng and Li, Hengli and Zhao, Yanpeng and Li, Chenxi and Wu, Huimin and Ma, Xiaojian and Zhu, Song-Chun and Wu, Ying Nian and Li, Qing},
  journal={arXiv preprint arXiv:2509.22761},
  year={2025}
}